Factorials!

People sometimes ask me, "How do you write a factorial function in C++?"

Now there's some mighty fine theoretical answers to this question that you can learn in CompSci101, and those answers may very well be useful in your next job interview.  But what if you're trying to compute the relative strength of poker hands, or calculate odds in state lotteries?  Or perhaps you're interested in the probabilities of encountering a hash collision?  What if what you really want is a function that returns factorials?

What if you want this function, but with less bugs:

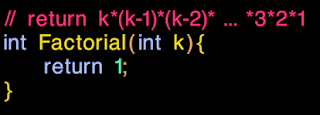Super fast and super accurate, iff k<=1

If you've been following along at home, you know that we can write a program to help write a factorial function for us.

Here's one I prepared earlier:

Could we write this in Python?  Probably not; we need bug-compatiblity with C++.

Here's the output:

    int factorialTable[]={1,
        1,//1!
        2,//2!
        6,//3!
        24,//4!
        120,//5!
        720,//6!
        5040,//7!
        40320,//8!
        362880,//9!
        3628800,//10!
        39916800,//11!
        479001600,//12!
        1932053504,//13!  <- Uh oh!
        1278945280,//14!
        2004310016,//15!
        ...

Uh oh, 13! == 6,227,020,800.  Something isn't quite right.  This number is larger than INT_MAX == 2,147,483,647.  It's simply too big to fit in a 32 bit integer.

Lets finish the function anyway, and then see what we need to change :

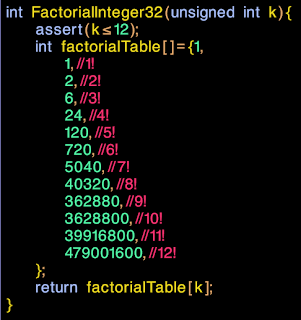Fast and accurate, iff k<=12

This is probably just fine for calculating our spherical harmonics coefficients, but it looks like we might be stuck when it comes to poker.

We could try move to 64 bit integers, but that will just slow everything down.  Lets try to move to floating point instead, and see what happens:

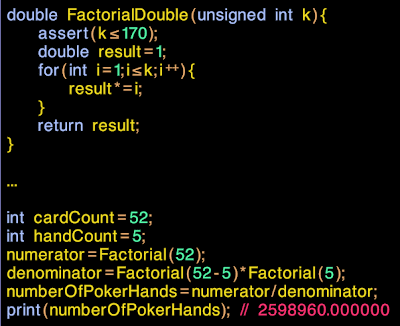Great! Now we can approximate factorials all the way up to 170!

Of course, we're only using approximations to factorials now, so lets compute the error term.

Here's the actual 52!

80658175170943878571660636856403766975289505440883277824000000000000

And this is the return value from Factorial(52) when expressed as a double :

80658175170944942000000000000000000000000000000000000000000000000000

Around 13 significant figures, which is reasonable for double precision.

Now lets look at numberOfPokerHands. A quick check on wikipedia reveals that there are indeed 2,598,690 different poker hands, so it's all good.  But wait, the value of numberOfPokerHands is coming out as exactly 2,598,690.0000000...  A quickwatch in the debugger reveals there is no error term at all.

No error term at all???  How can this be??

Somehow we're getting an exact result, even though we did a whole bunch of floating-point math, and almost all our intermediate quantities had to be rounded.

The trick is that the errors in the numerator and in the denominator are correlated.  They both contain the same errors.  When we divide one by the other, all the common factors cancel out, and all the common error terms cancel out too.

If you're playing along at home, you might try to write a version of FactorialDouble where the errors don't correlate.  Hint : You might need to invoke the optimizer.

 

Bigger

 

So now we can go up to 170!, the largest factorial representable in double precision floating point.

What if we want to go bigger still? Say, 365, the number of days in a year.  Or, 416, the number of passengers on a jumbo jet.

Let's use the slide-rule technique, and work with the log of our numbers, instead of the numbers themselves. In this scheme, we add the log of two numbers to multiply, and we subtract to divide.

Like this:

If you try and speed this up, be sure that you're careful to keep our special error correlation property.

Speed or Accuracy?

You can see a fairly typical progression throughout this post.  We started out with an extremely fast function, that worked correctly for a very narrow range of inputs.  As we increased the range, the function got slower and then approximate, and ultimately ended up returning a mapping of the desired output.

But even using this approximate form, we can still obtain exact results for a large range of interesting problems, by careful handling of our error terms.

When developing algorithms, we see these kind of trade-offs again and again.  I'd love to hear about some you've encountered in the comments below.

Appendix - Factorial functions in C++

If you're just looking for code, the following three "Factorial" functions are hereby licensed under CC0.

---

//From http://missingbytes.blogspot.com/2012/04/factorials.html
int FactorialInteger32(unsigned int k){
    assert(k<=12);
    int factorialTable[]={1,
        1,//1!
        2,//2!
        6,//3!
        24,//4!
        120,//5!
        720,//6!
        5040,//7!
        40320,//8!
        362880,//9!
        3628800,//10!
        39916800,//11!
        479001600,//12!
    };
    return factorialTable[k];
}

double FactorialDouble(unsigned int k){
    assert(k<=170);
    if(k<=12){
        return FactorialInteger32(k);
    }
    double result=FactorialInteger32(12);
    for(int i=13;i<=k;i++){
        result*=i;
    }
    return result;
}

double LogFactorial(unsigned int k){
    if(k<=170){
        return log(FactorialDouble(k));
    }
    double result=log(FactorialDouble(170));
    for(int i=171;i<=k;i++){
        result+=log(i);
    }
    return result;
}